Wat is een seriegrootte?

Een van de belangrijkste vragen die Voorraadbeheer moet beantwoorden is: ”In welke seriegrootte moeten we bestellen/produceren?” Eerst kijken we naar seriegroottebepalingen in handelsomgevingen, daarna naar seriegroottebepalingen in productieomgevingen.

1. Seriegroottebepaling in (groot)handelsomgevingen

Als we bijvoorbeeld per jaar 6000 stuks van product A moeten inkopen bij een leverancier; doen we dat in serie van 1 stuks of 6000 stuks of in een andere bestelserie? Gevoelsmatig weet u meteen al dat een serie van 1 stuks (te vaak bestellen) of 6000 stuks (te veel voorraad) niet optimaal zullen zijn. In een handelsomgeving minimaliseert de optimale seriegrootte de som van

• de totale bestelkosten (=aantal bestellingen x bestelkosten per bestelling)
• de totale voorraadkosten (= gemiddelde voorraad/jaar x voorraadkosten)
• de totale inkoopkosten (totaal aantal producten per jaar x inkoopprijs)

De seriegrootte bepaling is een trade-off op basis van kosten, maar dan moeten we deze kosten wel kennen. En met name voor bestel- en voorraadkosten blijkt dat in praktijk nog niet zo eenvoudig te zijn. Verder is de seriegrootte bepaling afhankelijk van het vraag(afzet)patroon. Hier kunnen we de volgende vraagpatronen onderscheiden:

• Regelmatige afzet
• Onregelmatige afzet maar bekend
• Onregelmatige afzet maar onbekend

Maar ook de belangrijkheid van een product al een rol spelen. Bij laagwaardige producten zullen we iets anders doen dan bij dure hoogwaardige producten.

Schematisch vinden we dan het volgende overzicht

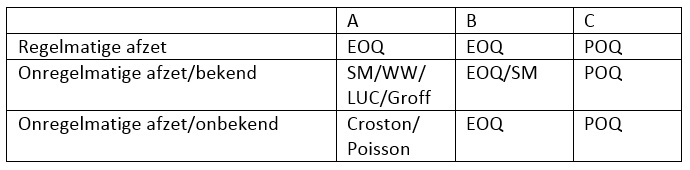
De verschillende methodieken in een notendop.

Economic Order Quantity (EOQ)
De EOQ methode, ook wel de formule van Camp, genoemd is meer dan 100 jaar oud en ‘uitgevonden’ door Harris in 1913. Deze methode zoekt in de oorspronkelijke vorm naar het minimum van totale kosten plus bestelkosten en ziet er als volgt uit:

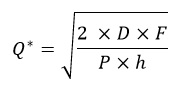
De EOQ kan aangepast worden voor situaties met kwantum/staffelkorting en beperkingen (bijvoorbeeld beperkte ruimte, beperkte houdbaarheid etc). Het charmante van de EOQ aanpak is dat de methode erg ongevoelig is voor fouten in de parameters. Stel dat de optimale seriegrootte Q* minimale kosten oplevert van C*. Wanneer we echter een seriegrootte Q gebruiken die afwijkt van Q* dan krijgen we natuurlijk hogere kosten. We kunnen aantonen dat afwijkingen van 25% t.o.v. de optimale seriegrootte leiden tot afwijkingen van minder dan 5% t.o,v, de minimale kosten.

1.1 POC (Periodic Order Quantity)

De POC-methode wordt gebruikt voor goedkope producten of voor producten die we niet veel aandacht willen geven. Dit soort producten wordt periodiek besteld, bijvoorbeeld eens per jaar, eens per half jaar etc. Het interval kan afgeleid worden uit de EOQ methode. Stel dat de vraag naar een product op 50 stuks per jaar wordt geschat. De EOQ zou voor dit product 8 zijn. Dan zouden we bijvoorbeeld elke 2 maanden er 9 kunnen bestellen, zonder naar de voorraad te kijken. Periodiek (bijv jaarlijks) kijken we naar de voorraad om te kijken of er een bestelling overgeslagen kan worden of dat er een extra bestelling geplaatst moet worden. In combinatie met een hoge veiligheidsvoorraad garandeert dit een hoge servicegraad. We ruilen hier als het ware beheerslast in tegen hogere voorraden.

1.2 SM/WW/LUC/Groff

Voor situaties met een onregelmatige maar bekende vraag komen methodieken als Silver-Meal, Wagner-Whitin, Least Unit Cost of Groff naar voren. Stel de afzet voor de komende 12 perioden is bekend zoals het voorbeeld in onderstaande tabel.

Naast de afzet zijn ook de bestelkosten per bestelling bekend en de kosten om één stuks één periode op voorraad te houden. De eerdergenoemde technieken werken nu allemaal volgens het volgende principe. Ik zit in periode 0 en ik heb besteld voor periode 1. Is het nu zinvol om ook voor periode 2 bij te bestellen? En zo ja is het dan ook zinvol om nu ook al periode 3 te bestellen? De Wagner-Whitin methodiek geeft voor dit probleem de optimale oplossing, maar is voor de leek een beetje ondoorzichtig en gevoelig als er tóch variaties in de afzet zijn.

1.3 Croston en de Poisson-aanpak

Deze methoden zijn bedoeld voor omgevingen met een lumpy demand (nu en dan eens een afzet). Het moment waarop de vraag optreedt is niet bekend en de afzet ook niet. Vooral als de producten erg duur zijn en/of een lange levertijd hebben kan dit problematisch zijn. We vinden dit soort vraagpatronen terug in spare-parts omgevingen. Een summiere uitwerking van de principes van de methodieken is als volgt. Stel dat er nú een vraag naar het product is geweest.

Croston kijkt naar de afzet in het verleden en voorspelt op basis daarvan wanneer het volgende afzetmoment is en vervolgens hoe groot die afzet gaat worden.

De Poisson benadering bepaalt de kans dat er binnen de levertijd van het product er 0,1,2, producten gevraagd gaan worden. Dit onder de voorwaarde dat de afzet een Poisson benadering volgt, dat een redelijke veronderstelling als van een product maar een paar stuks per jaar gevraagd worden.

2. Seriegrootte in productie-omgevingen

Het bepalen van seriegroottes in productie omgevingen kan in principe op dezelfde manier gaan als in handelsomgevingen maar levert toch enkele theoretische problemen op.

Het eerste probleem is het bepalen van de omstelkosten. Met name wanneer de machine overcapaciteit heeft. Wat zijn dan de kosten verbonden aan een omstelling?

Het tweede probleem, bij een routing over verschillende werkplekken/machines, dat het kan betekenen dat we pér machine een verschillende productieserie krijgen. Dit kan men oplossen om alleen voor de bottle-neck machine de seriegrootte te bepalen en deze te gebruiken voor de hele afdeling. Dit kan echter een derde probleem uitlokken dat met name ook speelt in de procesindustrie.

Het derde probleem is het zogenaamde interferentie-probleem dat gaat optreden als we voor verschillende producten die over één machine gaan de seriegroottes gaan berekenen. Omdat de series pér afzonderlijk product berekend worden, houdt men geen samenhang met de seriegroottes van andere producten. Dat kan gevolgen hebben voor de cyclustijden van de diverse producten.

Een vierde probleem dat hier mee samenhangt dat het zou bijvoorbeeld kunnen betekenen dat de totale bewerkingstijd en omsteltijden voor alle producten tesamen groter zijn dan de beschikbare capaciteit.